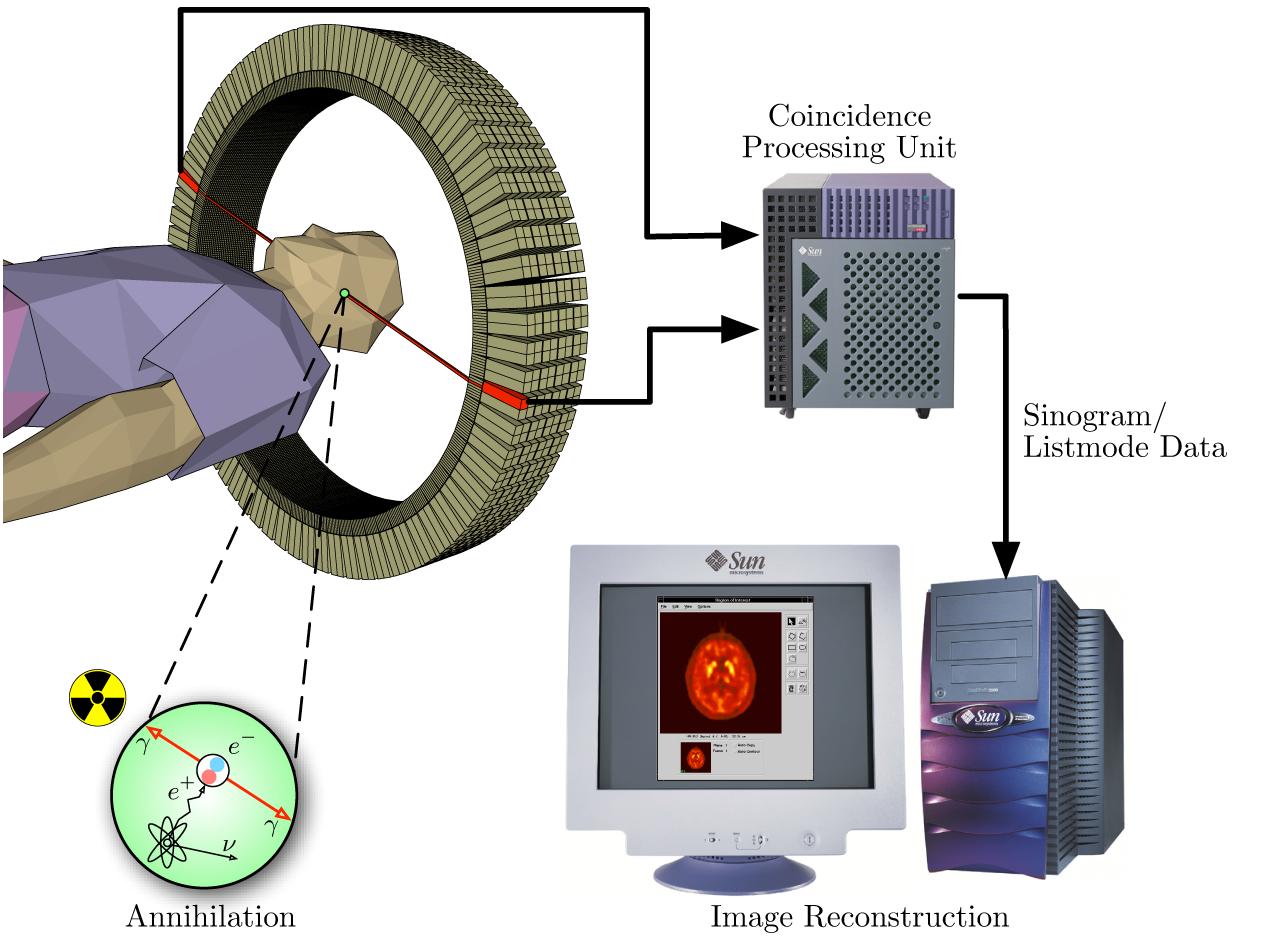
1. Introduction to MRI and Tomography

1.1 MRI Overview

MRI scan and CT scan use different technology to create diagnostic images of your body. MRI uses radio waves, while CT uses x-rays.

Magnetic Resonance Imaging (MRI) is a non-invasive imaging technique used to visualize the internal structures of the body, especially soft tissues such as the brain, muscles, and organs. MRI uses magnetic fields and radiofrequency waves to manipulate the behavior of hydrogen atoms, which are abundant in the human body due to the high water content of tissues.

When a patient is placed in a strong magnetic field, the hydrogen nuclei (protons) in their body align with the magnetic field. A radiofrequency pulse is then applied, causing the protons to flip from their alignment. Once the radiofrequency pulse is turned off, the protons return to their original alignment, emitting signals that can be detected and used to create images.

The mathematical process behind MRI involves reconstructing images from these signals, which are acquired in the frequency domain. The images are produced through complex mathematical operations such as Fourier transforms, inversion algorithms, and optimization techniques.

1.2 Tomography Overview

Tomography refers to a collection of techniques that create detailed cross-sectional images of the body. It is used to study structures inside the body by taking slices or sections, which can then be combined into a 3D model. MRI is one form of tomography, but other techniques like X-ray tomography (CT scanning), positron emission tomography (PET), and ultrasound also fall under this category.

In all types of tomography, the key mathematical challenge is reconstructing an image from data collected from multiple angles or positions. This is often referred to as "tomographic reconstruction," and it relies heavily on advanced mathematical algorithms.

2. The Mathematical Foundations of MRI

2.1 The Role of Fourier Transform

The core mathematical tool used in MRI is the Fourier transform. The MRI machine does not directly capture spatial information about the tissue; rather, it collects data in the frequency domain. Specifically, MRI measures the signals in k-space, which is a mathematical representation of spatial frequencies. To reconstruct the image, these frequency-domain signals are converted back to the spatial domain using a process called inverse Fourier transform.

In simple terms, a Fourier transform breaks down complex signals into simpler sinusoidal components of different frequencies. These frequencies are then used to reconstruct an image. The use of Fourier transforms in MRI allows for high-speed data processing and image reconstruction.

In MRI, this process allows the conversion of data from k-space back into an image representation of the body.

2.2 k-Space and Data Acquisition

MRI scanners acquire data in k-space, a mathematical domain that represents spatial frequencies. Each point in k-space corresponds to a specific spatial frequency component of the final image. The resolution of the MRI image is determined by how densely data points are sampled in k-space.

K-space is typically represented in polar coordinates, with the central part of k-space corresponding to low-frequency components (which affect the image's contrast), while the outer regions correspond to high-frequency components (which affect the image's resolution and fine details).

Data is acquired by varying the gradient magnetic fields in different directions (x, y, and z axes), which results in the sampling of different points in k-space. Once all data points have been collected, the inverse Fourier transform is applied to reconstruct the image.

2.3 Image Reconstruction Algorithms

Image reconstruction in MRI involves mathematical algorithms that convert the raw data (acquired from k-space) into a visual image. Some of the most commonly used algorithms include:

Backprojection: In this method, data is backprojected onto the image grid, which is essentially a simple form of tomography. However, it is computationally inefficient and rarely used for advanced MRI imaging today.
Iterative Reconstruction: This method involves a series of iterations to refine the image. The algorithm starts with an initial guess for the image and iteratively adjusts it based on the acquired data. This process is highly computational but can provide higher-quality images.
Radon Transform and Inversion: The Radon transform is a mathematical operator used to convert an image into projections (i.e., the sum of pixel values along different lines). It plays a vital role in reconstructing images from projections in tomography. The inverse Radon transform is used to convert the projections back into the original image.

2.4 The Challenge of Artifacts

Artifacts in MRI images can occur due to various factors, including patient movement, magnetic field inhomogeneity, or insufficient sampling of k-space. The mathematics behind MRI also involves techniques to mitigate or correct these artifacts, such as:

Motion Correction Algorithms: These algorithms are used to compensate for patient movement during scanning, ensuring that the acquired data is accurate.

Compressed Sensing: This advanced mathematical approach reduces the amount of data needed to reconstruct an image by exploiting sparsity in the image. It allows for faster scanning times while still maintaining image quality.

3. The Mathematics of Tomography

3.1 The Radon Transform

The Radon transform is the primary mathematical operation in tomography. It is a way of representing an image as a set of projections. In 2D tomography, the Radon transform takes an image and produces its projections.

This process is used to represent the image as a collection of line integrals (projections). To reconstruct the original image, the inverse Radon transform is applied, which is a key component of tomographic reconstruction algorithms.

3.2 The Inverse Problem

In tomography, the goal is to solve the inverse problem: given the projections (which are integrals of the original image along various directions), how can the original image be reconstructed? This problem is ill-posed, meaning that there is no unique solution in the strict mathematical sense, and small errors in the data can lead to large variations in the reconstructed image.

One approach to solving the inverse problem is filtered backprojection, which involves applying a filter to the projections to remove noise and then backprojecting them to obtain an image. While this method is commonly used in CT imaging, it can also be adapted to MRI with appropriate modifications.

3.3 Algorithms for Tomographic Reconstruction

Several mathematical algorithms are used for tomographic reconstruction. These include:

Filtered Backprojection (FBP): This is the standard algorithm used in X-ray tomography (CT). It involves applying a filter to the raw data to enhance high-frequency information, followed by backprojection to reconstruct the image.
Iterative Reconstruction: This algorithm refines the image iteratively by comparing the reconstructed image to the original data and adjusting it to minimize the error. This method is computationally expensive but can produce higher-quality images.
Algebraic Reconstruction Techniques (ART): ART is an iterative method that updates the image in small steps, reducing the difference between the projections and the measured data.

3.4 Advanced Methods: Compressed Sensing and Machine Learning

With the development of more advanced computing power and algorithms, techniques like compressed sensing and machine learning are beginning to play a significant role in improving tomographic reconstruction. Compressed sensing is a technique that allows for faster scanning by acquiring fewer data points, while machine learning algorithms can help improve image quality by learning patterns in the data and applying them to reconstruct images.

Compressed sensing works by exploiting the sparsity of signals. If the data or image can be represented sparsely in some transform domain, it is possible to recover the image from fewer samples than traditionally required. The key mathematical principle behind compressed sensing is to solve an optimization problem.

Machine learning methods, such as deep learning, have been employed to optimize tomographic reconstruction by training neural networks to predict missing or noisy data, improving the quality and speed of image reconstruction.

4. Conclusion

The mathematics of MRI and tomography is a complex and fascinating area of study that integrates advanced concepts from Fourier analysis, integral geometry, optimization, and numerical methods. The mathematical principles behind MRI and tomography not only allow for the reconstruction of high-quality medical images but also enable significant advances in imaging techniques, such as reduced scanning times, improved image resolution, and better noise reduction.

As technology advances, the application of machine learning and compressed sensing will likely continue to transform the field, offering even faster and more accurate imaging methods. Understanding the mathematical foundation of these techniques is crucial for appreciating their impact on modern medicine and the potential they hold for future diagnostic capabilities.